728x90
# 라이브러리 임포트
import tensorflow.keras
from keras.models import Sequential
from keras.lavers import Dense# 딥러닝을 이용한 모델링
model = Swquential()
X_train.shape # 첫번째 히든레이어의 인풋 레이어의 숫자 셋팅을 위해 확인
(400, 5)# 첫번째 히든레이어 생성 : 이때는 인풋 레이어의 숫자도 셋팅해준다. input_dim = 5
model.add( Dense(units = 20, activation = 'relu', input_dim = 5 ) )# 두번째 히든레이어 생성
model.add( Dense(units = 10, activation = 'relu'))# 아웃풋 레이어 생성
# 리그레션 문제의 액티베이션 펑션은 linear 사용
model.add( Dense(units = 1, activation = 'linear'))# 만든 모델을, 요약
model.summary()
# 결과값
Model: "sequential_1"
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
dense_3 (Dense) (None, 20) 120
dense_4 (Dense) (None, 10) 210
dense_5 (Dense) (None, 1) 11
=================================================================
Total params: 341
Trainable params: 341
Non-trainable params: 0
_________________________________________________________________# 옵티마이저는 'adam' 으로 하고, 로스펑션은 'mean_squared_error' 로 셋팅하여 컴파일
# 컴파일(Compile) ?
# 오차함수를 설정하고, 옵티마이저(그레디언트 디센트 알고리즘)를 설정한다.
# 옵티마이저는, 그레디언트 디센트 알고리즘을 개선한 것들 중에서 선택하면 된다.
# 그레디언트 디센트는, 오차가 최소가 될때의 W 값을 찾는 알고리즘이다.
# loss 는, 오차함수를 말한다.
model.compile(optimizer = 'adam', loss = 'mean_squared_error')
# 'mean_squared_error' = MSE# 컴파일이 끝나면, 학습을 진행.
epoch_history = model.fit(X_train, y_train, batch_size=20, epochs=20 ) # 학습 데이터의 결과
# 출력
Epoch 1/20
20/20 [==============================] - 0s 1ms/step - loss: 0.0210
Epoch 2/20
20/20 [==============================] - 0s 1ms/step - loss: 0.0105
Epoch 3/20
20/20 [==============================] - 0s 1ms/step - loss: 0.0079
Epoch 4/20
20/20 [==============================] - 0s 2ms/step - loss: 0.0062
Epoch 5/20
20/20 [==============================] - 0s 1ms/step - loss: 0.0052
Epoch 6/20
20/20 [==============================] - 0s 1ms/step - loss: 0.0044
Epoch 7/20
20/20 [==============================] - 0s 1ms/step - loss: 0.0035
Epoch 8/20
20/20 [==============================] - 0s 1ms/step - loss: 0.0028
Epoch 9/20
20/20 [==============================] - 0s 1ms/step - loss: 0.0021
Epoch 10/20
20/20 [==============================] - 0s 1ms/step - loss: 0.0016
Epoch 11/20
20/20 [==============================] - 0s 1ms/step - loss: 0.0012
Epoch 12/20
20/20 [==============================] - 0s 1ms/step - loss: 9.1913e-04
Epoch 13/20
20/20 [==============================] - 0s 2ms/step - loss: 7.3311e-04
Epoch 14/20
20/20 [==============================] - 0s 1ms/step - loss: 5.6759e-04
Epoch 15/20
20/20 [==============================] - 0s 1ms/step - loss: 4.6450e-04
Epoch 16/20
20/20 [==============================] - 0s 1ms/step - loss: 3.7364e-04
Epoch 17/20
20/20 [==============================] - 0s 1ms/step - loss: 3.1415e-04
Epoch 18/20
20/20 [==============================] - 0s 2ms/step - loss: 2.6817e-04
Epoch 19/20
20/20 [==============================] - 0s 1ms/step - loss: 2.4016e-04
Epoch 20/20
20/20 [==============================] - 0s 1ms/step - loss: 2.1935e-04# 테스트셋으로 예측
y_pred = model.predict(X_test)
# MSE 계산
# MSE : 오차를 구하고, 제곱한 후, 평균을 구한다.
# Mean, Squared, Error
((y_test - y_pred) ** 2).mean()
# 출력
0.00033102419183589203# 실제값과 예측값을 plot 으로 나타내기
plt.plot(y_test)
plt.plot(y_pred)
plt.legend(['Real','Pred'])
plt.show()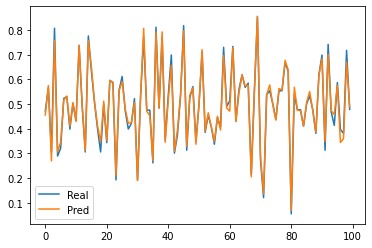
'Python' 카테고리의 다른 글
| 이미지를 피처 스케일링 하는 방법 (0) | 2021.12.01 |
|---|---|
| 이미지의 행렬, Gray Scale Image. Color Image (0) | 2021.12.01 |
| 원 핫 인코딩 Dummy variable trap (0) | 2021.11.30 |
| 딥러닝 옵티마이저(Optimizer) 종류, 발달 계보 (0) | 2021.11.30 |
| 파이썬 Prophet 라이브러리 사용법 (0) | 2021.11.29 |